When data gets complicated, it's often because it lives in more dimensions than we can imagine. But what looks messy at first may just be a simple structure hiding under layers of extra information. Locally linear embedding (LLE) is a technique that tries to reveal those hidden shapes. It does this not by flattening the data or cutting corners but by listening to how points relate to their nearest neighbors.

This approach works well when the data lies on a curved or manifold surface within a much larger space. Instead of focusing on the big picture, LLE focuses on small, local relationships and rebuilds the overall shape from the ground up.

What Is Locally Linear Embedding?

LLE is a method for nonlinear dimensionality reduction. It helps uncover patterns in high-dimensional data by assuming that each point lives on a curved surface and can be understood using only its nearby neighbors. Traditional techniques like Principal Component Analysis (PCA) focus on global variance and often miss curved or twisted structures. LLE avoids that by focusing strictly on local information.

Suppose your data has thousands of features—like pixels in an image. While the raw numbers live in high-dimensional space, the true variation in the images (like pose or expression) might only span two or three dimensions. LLE looks at each point, finds a handful of nearby points, and writes the point as a weighted sum of its neighbors. These weights reconstruct a lower-dimensional data version that keeps those same relationships intact.

The result is a clean, reduced version of your data that keeps the same local geometry but discards the extra bulk. This helps make complex data understandable and visualizable while staying true to its original structure.

How Does It Work Behind the Scenes?

The LLE algorithm runs in three stages. First, it finds the k closest points in high-dimensional space for each data point. These neighbors define the point's local context. Choosing the right k is important: too small and you miss detail; too large and you introduce noise.

Next, it calculates weights that describe how to recreate the point using just its neighbors. This step involves solving a set of linear equations, where the weights are picked to minimize the difference between the actual point and the weighted combination of its neighbors. These weights are local—they don’t depend on the final lower-dimensional shape, only on the original high-dimensional data.

Finally, the algorithm finds a new set of points in a lower-dimensional space that preserves these weights. The idea is that the same local relationships should be held in smaller spaces. This embedding step involves solving another equation to lay out the data in fewer dimensions while maintaining those neighborhood structures.

The key idea behind LLE is that if points sit near each other on a curved surface in high-dimensional space, they'll still relate similarly once the surface is unrolled into fewer dimensions. This allows complex data to be simplified without forcing it into artificial patterns.

Practical Applications and Limits

LLE is useful in situations where data is high-dimensional but contains local structure. For example, each face might have thousands of pixel values in facial image datasets. But all those images can often be explained by just a few factors—like the person's pose or lighting direction. These changes form a smooth curve in high-dimensional space, which LLE can untangle into something much easier to explore.

Another use case is human motion capture data. Even though sensors record dozens of body joint angles, most human movements are governed by a few repeating patterns. LLE can reduce the full-body motion data into a smaller number of meaningful variables, like walking cycles or arm swings.

Still, LLE has limits. It depends heavily on the quality of local neighborhoods. Those local estimates can become unreliable if your data has gaps, noise, or outliers. Picking the wrong number of neighbors can also skew the results. A k value that's too small may lead to disconnected results, while a value that is too large can stretch the structure.

There’s also the matter of size. LLE doesn’t scale well to massive datasets because it involves matrix operations that become slow and memory-hungry. For small to medium-sized problems, though, it remains a strong choice.

LLE vs. Other Dimensionality Reduction Methods

Compared to other dimensionality reduction methods, LLE holds its own by sticking to what's local. PCA, a classic method, projects data in directions of maximum variance. It’s quick but only handles linear data. Curved shapes or folds confuse it.

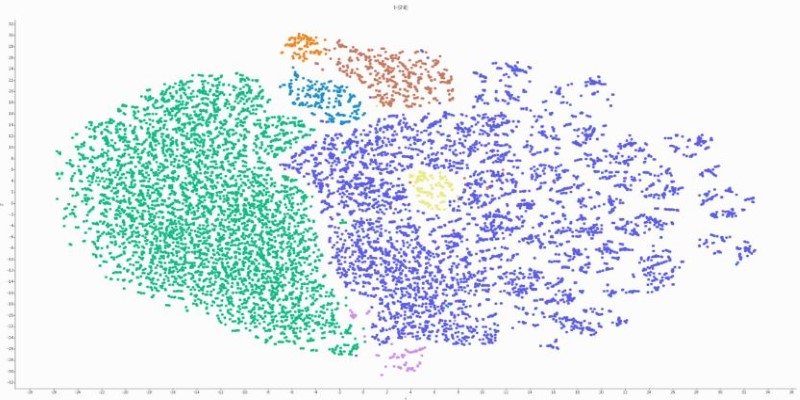
t-SNE is a newer method known for its visual plots. It focuses on preserving how likely two points are to be near each other. While it produces striking visualizations, t-SNE doesn’t maintain a meaningful global structure and often struggles with reproducibility.

Isomap, another manifold technique, preserves global distances by measuring paths through the data graph. It works well in theory but becomes fragile when the data is noisy or disconnected.

What makes LLE different is its quiet focus on local geometry. It doesn't force data into clusters or guess at large-scale structures. It keeps relationships grounded in what the data already shows. That's a good fit when your data doesn't follow a simple formula but still behaves predictably within its small neighborhoods.

Conclusion

Locally Linear Embedding helps untangle high-dimensional data by working from the inside out. It doesn't try to control the whole shape or make sweeping assumptions. Instead, it focuses on how each point fits into its neighborhood and uses those relationships to build a clearer picture. This approach works well when the data has a hidden, low-dimensional form that isn't easy to spot. LLE keeps things honest: it trusts the data to show its structure and follows that lead. While it's not a one-size-fits-all tool, it remains one of the more thoughtful methods in the dimensionality reduction toolbox.